Proposition: 5.09: Magnitudes with Same Ratios are Equal

(Proposition 9 from Book 5 of Euclid's “Elements”)

(Magnitudes) having the same ratio to the same (magnitude) are equal to one another. And those (magnitudes) to which the same (magnitude) has the same ratio are equal.

For let $A$ and $B$ each have the same ratio to $C$.
I say that $A$ is equal to $B$.
So, again, let $C$ have the same ratio to each of $A$ and $B$.
I say that $A$ is equal to $B$.

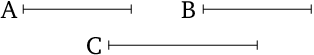
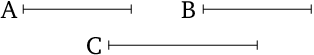
fig09e

Modern Formulation

In modern notation, this proposition reads that if $\alpha =\beta$ then \[\frac\alpha\gamma = \frac\beta\gamma\] and if \[\frac\gamma\alpha = \frac\gamma\beta\] then $\alpha =\beta$ for all positive real numbers $\alpha,\beta,\gamma$.

Generalized Formulation

The above proposition is true for all real numbers with $\alpha\neq 0, \beta\neq 0, \gamma\neq 0$, since it follows from the existence and uniqueness of inverse real numbers with respect to multiplication.

Proofs: 1

Proofs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Sections: 17