Proof: By Euclid

Let $AB$ and $CD$ be equal parallelepiped solids.
I say that the bases of the parallelepiped solids $AB$ and $CD$ are reciprocally proportional to their heights, and (so) as base $EH$ is to base $NQ$, so the height of solid $CD$ (is) to the height of solid $AB$.

fig34e

For, first of all, let the (straight lines) standing up, $AG$, $EF$, $LB$, $HK$, $CM$, $NO$, $PD$, and $QR$, be at right angles to their bases.
I say that as base $EH$ is to base $NQ$, so $CM$ (is) to $AG$.
Therefore, if base $EH$ is equal to base $NQ$, and solid $AB$ is also equal to solid $CD$, $CM$ will also be equal to $AG$.
For parallelepiped solids of the same height are to one another as their bases [Prop. 11.32].
And as base $EH$ (is) to $NQ$, so $CM$ will be to $AG$.
And (so it is) clear that the bases of the parallelepiped solids $AB$ and $CD$ are reciprocally proportional to their heights.
So let base $EH$ not be equal to base $NQ$, but let $EH$ be greater.
And solid $AB$ is also equal to solid $CD$.
Thus, $CM$ is also greater than $AG$.
Therefore, let $CT$ be made equal to $AG$.
And let the parallelepipedal solid $VC$ have been completed on the base $NQ$, with height $CT$.
And since solid $AB$ is equal to solid $CD$, and $CV$ (is) extrinsic (to them), and equal (magnitudes) have the same ratio to the same (magnitude) [Prop. 5.7], thus as solid $AB$ is to solid $CV$, so solid $CD$ (is) to solid $CV$.
But, as solid $AB$ (is) to solid $CV$, so base $EH$ (is) to base $NQ$.
For the solids $AB$ and $CV$ (are) of equal height [Prop. 11.32].
And as solid $CD$ (is) to solid $CV$, so base $MQ$ (is) to base $TQ$ [Prop. 11.25], and $CM$ to $CT$ [Prop. 6.1].
And, thus, as base $EH$ is to base $NQ$, so $MC$ (is) to $AG$.
And $CT$ (is) equal to $AG$.
And thus as base $EH$ (is) to base $NQ$, so $MC$ (is) to $AG$.
Thus, the bases of the parallelepiped solids $AB$ and $CD$ are reciprocally proportional to their heights.
So, again, let the bases of the parallelepipid solids $AB$ and $CD$ be reciprocally proportional to their heights, and let base $EH$ be to base $NQ$, as the height of solid $CD$ (is) to the height of solid $AB$.
I say that solid $AB$ is equal to solid $CD$.
For let the (straight lines) standing up again be at right angles to the bases.
And if base $EH$ is equal to base $NQ$, and as base $EH$ is to base $NQ$, so the height of solid $CD$ (is) to the height of solid $AB$, the height of solid $CD$ is thus also equal to the height of solid $AB$.
And parallelepiped solids on equal bases, and also with the same height, are equal to one another [Prop. 11.31].
Thus, solid $AB$ is equal to solid $CD$.
So, let base $EH$ not be equal to [base] $NQ$, but let $EH$ be greater.
Thus, the height of solid $CD$ is also greater than the height of solid $AB$, that is to say $CM$ (greater) than $AG$.
Let $CT$ again be made equal to $AG$, and let the solid $CV$ have been similarly completed.
Since as base $EH$ is to base $NQ$, so $MC$ (is) to $AG$, and $AG$ (is) equal to $CT$, thus as base $EH$ (is) to base $NQ$, so $CM$ (is) to $CT$.
But, as [base] $EH$ (is) to base $NQ$, so solid $AB$ (is) to solid $CV$.
For solids $AB$ and $CV$ are of equal heights [Prop. 11.32].
And as $CM$ (is) to $CT$, so (is) base $MQ$ to base $QT$ [Prop. 6.1], and solid $CD$ to solid $CV$ [Prop. 11.25].
And thus as solid $AB$ (is) to solid $CV$, so solid $CD$ (is) to solid $CV$.
Thus, $AB$ and $CD$ each have the same ratio to $CV$.
Thus, solid $AB$ is equal to solid $CD$ [Prop. 5.9].
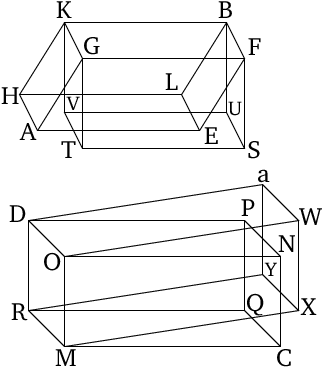
So, let the (straight lines) standing up, $FE$, $BL$, $GA$, $KH$, $ON$, $DP$, $MC$, and $RQ$, not be at right angles to their bases.
And let perpendiculars have been drawn to the planes through $EH$ and $NQ$ from points $F$, $G$, $B$, $K$, $O$, $M$, $R$, and $D$, and let them have joined the planes at (points) $S$, $T$, $U$, $V$, $W$, $X$, $Y$, and $a$ (respectively).
And let the solids $FV$ and $OY$ have been completed.
In this case, also, I say that the solids $AB$ and $CD$ being equal, their bases are reciprocally proportional to their heights, and (so) as base $EH$ is to base $NQ$, so the height of solid $CD$ (is) to the height of solid $AB$.
Since solid $AB$ is equal to solid $CD$, but $AB$ is equal to $BT$.
For they are on the same base $FK$, and (have) the same height [Prop. 11.29], [Prop. 11.30].
And solid $CD$ is equal is equal to $DX$.
For, again, they are on the same base $RO$, and (have) the same height [Prop. 11.29], [Prop. 11.30].
solid $BT$ is thus also equal to solid $DX$.
Thus, as base $FK$ (is) to base $OR$, so the height of solid $DX$ (is) to the height of solid $BT$ (see first part of proposition).
And base $FK$ (is) equal to base $EH$, and base $OR$ to $NQ$.
Thus, as base $EH$ is to base $NQ$, so the height of solid $DX$ (is) to the height of solid $BT$.
And solids $DX$, $BT$ are the same height as (solids) $DC$, $BA$ (respectively).
Thus, as base $EH$ is to base $NQ$, so the height of solid $DC$ (is) to the height of solid $AB$.
Thus, the bases of the parallelepiped solids $AB$ and $CD$ are reciprocally proportional to their heights.
So, again, let the bases of the parallelepiped solids $AB$ and $CD$ be reciprocally proportional to their heights, and (so) let base $EH$ be to base $NQ$, as the height of solid $CD$ (is) to the height of solid $AB$.
I say that solid $AB$ is equal to solid $CD$.
For, with the same construction (as before), since as base $EH$ is to base $NQ$, so the height of solid $CD$ (is) to the height of solid $AB$, and base $EH$ (is) equal to base $FK$, and $NQ$ to $OR$, thus as base $FK$ is to base $OR$, so the height of solid $CD$ (is) to the height of solid $AB$.
And solids $AB$, $CD$ are the same height as (solids) $BT$, $DX$ (respectively).
Thus, as base $FK$ is to base $OR$, so the height of solid $DX$ (is) to the height of solid $BT$.
Thus, the bases of the parallelepiped solids $BT$ and $DX$ are reciprocally proportional to their heights.
Thus, solid $BT$ is equal to solid $DX$ (see first part of proposition).
But, $BT$ is equal to $BA$.
For [they are] on the same base $FK$, and (have) the same height [Prop. 11.29], [Prop. 11.30].
And solid $DX$ is equal to solid $DC$ [Prop. 11.29], [Prop. 11.30].
Thus, solid $AB$ is also equal to solid $CD$.
(Which is) the very thing it was required to show.
∎

Thank you to the contributors under CC BY-SA 4.0!

Github:
non-Github:: @Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

Fitzpatrick, Richard: Euclid's "Elements of Geometry"

◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-11-elementary-stereometry / Proof: By Euclid

Proof: By Euclid

References

Adapted from (subject to copyright, with kind permission)