Proposition: 5.14: Relative Sizes of Components of Ratios

Euclid's Formulation

If a first (magnitude) has the same ratio to a second that a third (has) to a fourth, and the first (magnitude) is greater than the third, then the second will also be greater than the fourth. And if (the first magnitude is) equal (to the third then the second will also be) equal (to the fourth). And if (the first magnitude is) less (than the third then the second will also be) less (than the fourth).

For let a first (magnitude) $A$ have the same ratio to a second $B$ that a third $C$ (has) to a fourth $D$.
And let $A$ be greater than $C$.
I say that $B$ is also greater than $D$.

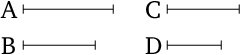
fig14e

Modern Formulation

In modern notation, this proposition reads that if \[\frac\alpha\beta=\frac\gamma\delta,\] then \[\alpha \gtreqqless \gamma~\text{ as }~\beta\gtreqqless\delta,\]

for all positive real numbers $\alpha,\beta,\gamma,\delta$.

Proofs: 1

Proofs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
Sections: 24