Proof: By Euclid

And, first of all, (let us prove) that the (rectangle contained) by $CBD$ [is] equal to the (square) on $BA$.

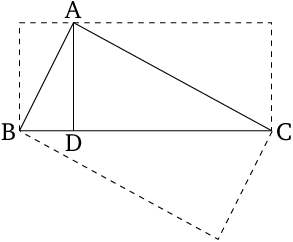
fig032ae

For since $AD$ has been drawn from the right angle in a right-angled triangle, perpendicular to the base, $ABD$ and $ADC$ are thus triangles (which are) similar to the whole, $ABC$, and to one another [Prop. 6.8].
And since triangle $ABC$ is similar to triangle $ABD$, thus as $CB$ is to $BA$, so $BA$ (is) to $BD$ [Prop. 6.4].
Thus, the (rectangle contained) by $CBD$ is equal to the (square) on $AB$ [Prop. 6.17].
So, for the same (reasons), the (rectangle contained) by $BCD$ is also equal to the (square) on $AC$.
And since if a (straight line) is drawn from the right angle in a right-angled triangle, perpendicular to the base, the (straight line so) drawn is in mean proportion3 to the pieces of the base [Prop. 6.8 corr.] 3, thus as $BD$ is to $DA$, so $AD$ (is) to $DC$.
Thus, the (rectangle contained) by $BD$ and $DC$ is equal to the (square) on $DA$ [Prop. 6.17].
I also say that the (rectangle contained) by $BC$ and $AD$ is equal to the (rectangle contained) by $BA$ and $AC$.
For since, as we said, $ABC$ is similar to $ABD$, thus as $BC$ is to $CA$, so $BA$ (is) to $AD$ [Prop. 6.4].
Thus, the (rectangle contained) by $BC$ and $AD$ is equal to the (rectangle contained) by $BA$ and $AC$ [Prop. 6.16].
(Which is) the very thing it was required to show.
∎

Thank you to the contributors under CC BY-SA 4.0!