◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-10-incommensurable-magnitudes / Lemma: Lem. 10.032: Constructing Medial Commensurable in Square II

Lemma: Lem. 10.032: Constructing Medial Commensurable in Square II

(Lemma to Proposition 32 from Book 10 of Euclid's “Elements”)

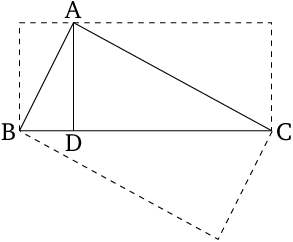
Let $ABC$ be a right-angled triangle having the (angle) $A$ a right angle. And let the perpendicular $AD$ have been drawn.

• I say that the (rectangle contained) by $CBD$ is equal to the (square) on $BA$, and the (rectangle contained) by $BCD$ (is) equal to the (square) on $CA$, and the (rectangle contained) by $BD$ and $DC$ (is) equal to the (square) on $AD$, and, further, the (rectangle contained) by $BC$ and $AD$ [is] equal to the (rectangle contained) by $BA$ and $AC$.

Modern Formulation

(not yet contributed)

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1 2 3

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"