◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-12-proportional-stereometry / Proposition: Prop. 12.16: Construction of Equilateral Polygon with Even Number of Sides in Outer of Concentric Circles

Proposition: Prop. 12.16: Construction of Equilateral Polygon with Even Number of Sides in Outer of Concentric Circles

Euclid's Formulation

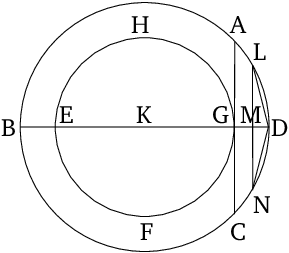
There being two circles about the same center, to inscribe an equilateral and even-sided polygon in the greater circle, not touching the lesser circle.

• Let $ABCD$ and $EFGH$ be the given two circles, about the same center, $K$.
• So, it is necessary to inscribe an equilateral and even-sided polygon in the greater circle $ABCD$, not touching circle $EFGH$.

Modern Formulation

(not yet contributed)

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016