Proof: By Euclid

Let $ABCD$ and $EFGH$ be the given two circles, about the same center, $K$.
So, it is necessary to inscribe an equilateral and even-sided polygon in the greater circle $ABCD$, not touching circle $EFGH$.

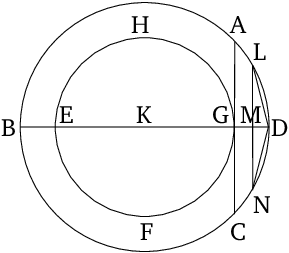
fig16e

Let the straight line $BKD$ have been drawn through the center $K$.
And let $GA$ have been drawn, at right angles to the straight line $BD$, through point $G$, and let it have been drawn through to $C$.
Thus, $AC$ touches circle $EFGH$ [Prop. 3.16 corr.] .
So, (by) cutting circumference $BAD$ in half, and the half of it in half, and doing this continually, we will (eventually) leave a circumference less than $AD$ [Prop. 10.1].
Let it have been left, and let it be $LD$.
And let $LM$ have been drawn, from $L$, perpendicular to $BD$, and let it have been drawn through to $N$.
And let $LD$ and $DN$ have been joined.
Thus, $LD$ is equal to $DN$ [Prop. 3.3], [Prop. 1.4].
And since $LN$ is parallel to $AC$ [Prop. 1.28], and $AC$ touches circle $EFGH$, $LN$ thus does not touch circle $EFGH$.
Thus, even more so, $LD$ and $DN$ do not touch circle $EFGH$.
And if we continuously insert (straight lines) equal to straight line $LD$ into circle $ABCD$ [Prop. 4.1] then an equilateral and even-sided polygon, not touching the lesser circle $EFGH$, will have been inscribed in circle $ABCD$.¹
(Which is) the very thing it was required to do.

∎

Thank you to the contributors under CC BY-SA 4.0!

Note that the chord of the polygon, $LN$, does not touch the inner circle either (translator's note). ↩