Proof: By Euclid

Let $AB$ be a straight line, and let it have been cut in extreme and mean ratio at $C$, and let $AC$ be the greater piece.
I say that the (sum of the squares) on $AB$ and $BC$ is three times the (square) on $CA$.

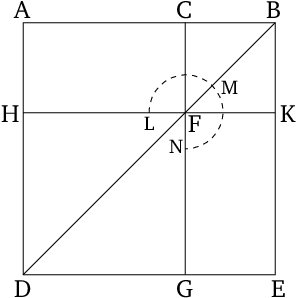
fig04e

For let the square $ADEB$ have been described on $AB$, and let the (remainder of the) figure have been drawn.
Therefore, since $AB$ has been cut in extreme and mean ratio at $C$, and $AC$ is the greater piece, the (rectangle contained) by $ABC$ is thus equal to the (square) on $AC$ [Def. 6.3] , [Prop. 6.17].
And $AK$ is the (rectangle contained) by $ABC$, and $HG$ the (square) on $AC$.
Thus, $AK$ is equal to $HG$.
And since $AF$ is equal to $FE$ [Prop. 1.43], let $CK$ have been added to both.
Thus, the whole of $AK$ is equal to the whole of $CE$.
Thus, $AK$ plus $CE$ is double $AK$.
But, $AK$ plus $CE$ is the gnomon $LMN$ plus the square $CK$.
Thus, gnomon $LMN$ plus square $CK$ is double $AK$.
But, indeed, $AK$ was also shown (to be) equal to $HG$.
Thus, gnomon $LMN$ plus [square $CK$ is double $HG$.
Hence, gnomon $LMN$ plus] the squares $CK$ and $HG$ is three times the square $HG$.
And gnomon $LMN$ plus the squares $CK$ and $HG$ is the whole of $AE$ plus $CK$ - which are the squares on $AB$ and $BC$ (respectively) - and $GH$ (is) the square on $AC$.
Thus, the (sum of the) squares on $AB$ and $BC$ is three times the square on $AC$.
(Which is) the very thing it was required to show.
∎

Thank you to the contributors under CC BY-SA 4.0!