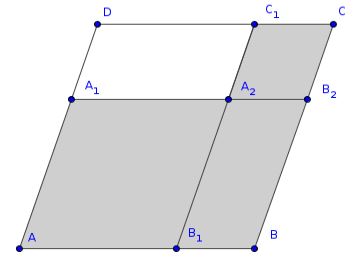
And in any parallelogrammic figure, let any one whatsoever of the parallelograms about its diagonal, (taken) with its two complements, be called1 a gnomon.
In a parallelogram \(\boxdot{ABCD}\) let \(\overline{AB}\parallel\overline{CD}\parallel\overline{A_1B_2}\) and \(\overline{AD}\parallel\overline{BC}\parallel\overline{B_1C_1}\), like shown in the following figure:
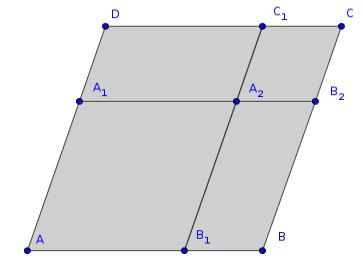
Then the four possible gnomons of the parallelogram are the gray-marked polygons:
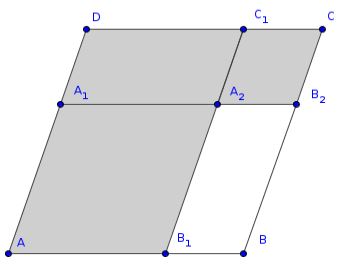
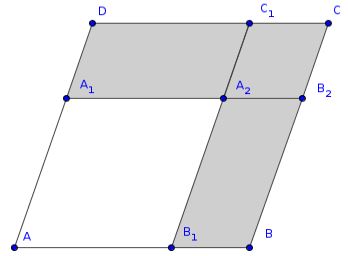
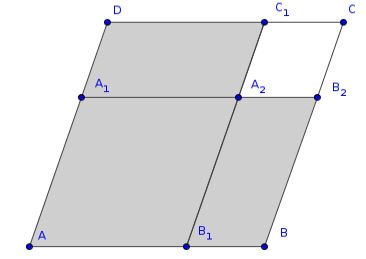

From Wikemedia
Proofs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
The name "gnomon" was probably chosen by Euclid because the figures in the parallelogram called gnomons are similar to the part of a sundial that casts a shadow: ↩