Let \(G(V,E,\gamma)\) be a biconnected graph and let \(C\) be a cycle in \(G\)1. \(G\) is planar, if and only if the following (recursive) conditions hold:
\((1)\) Every piece \(P\) of \(G\) with respect to \(C\) is planar, and
\((2)\) the interlacement graph \(I_C\) of the pieces of \(G\) with respect to \(C\) is bipartite.
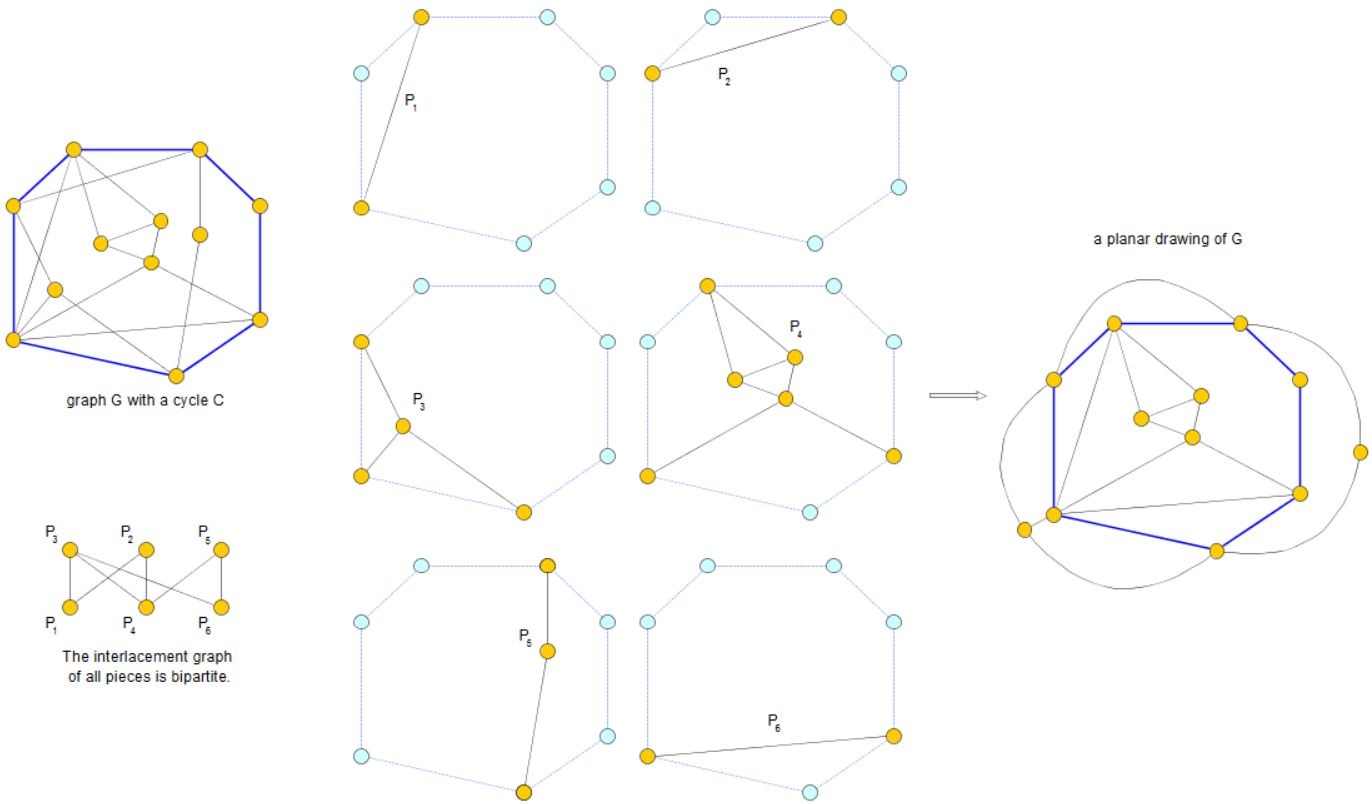
In the left-upper corner of the following figure, a graph \(G\) with a cycle (blue) is shown. The pieces of \(G\) with respect to this cycle are shown in the middle of the figure (\(P_1,P_2,\ldots,P_6\). The interlacement graph of these pieces (in the left-bottom corner) is bipartite. Since every piece of its own is planar, a planar drawing of \(G\) exists (shown on the right side of the figure):
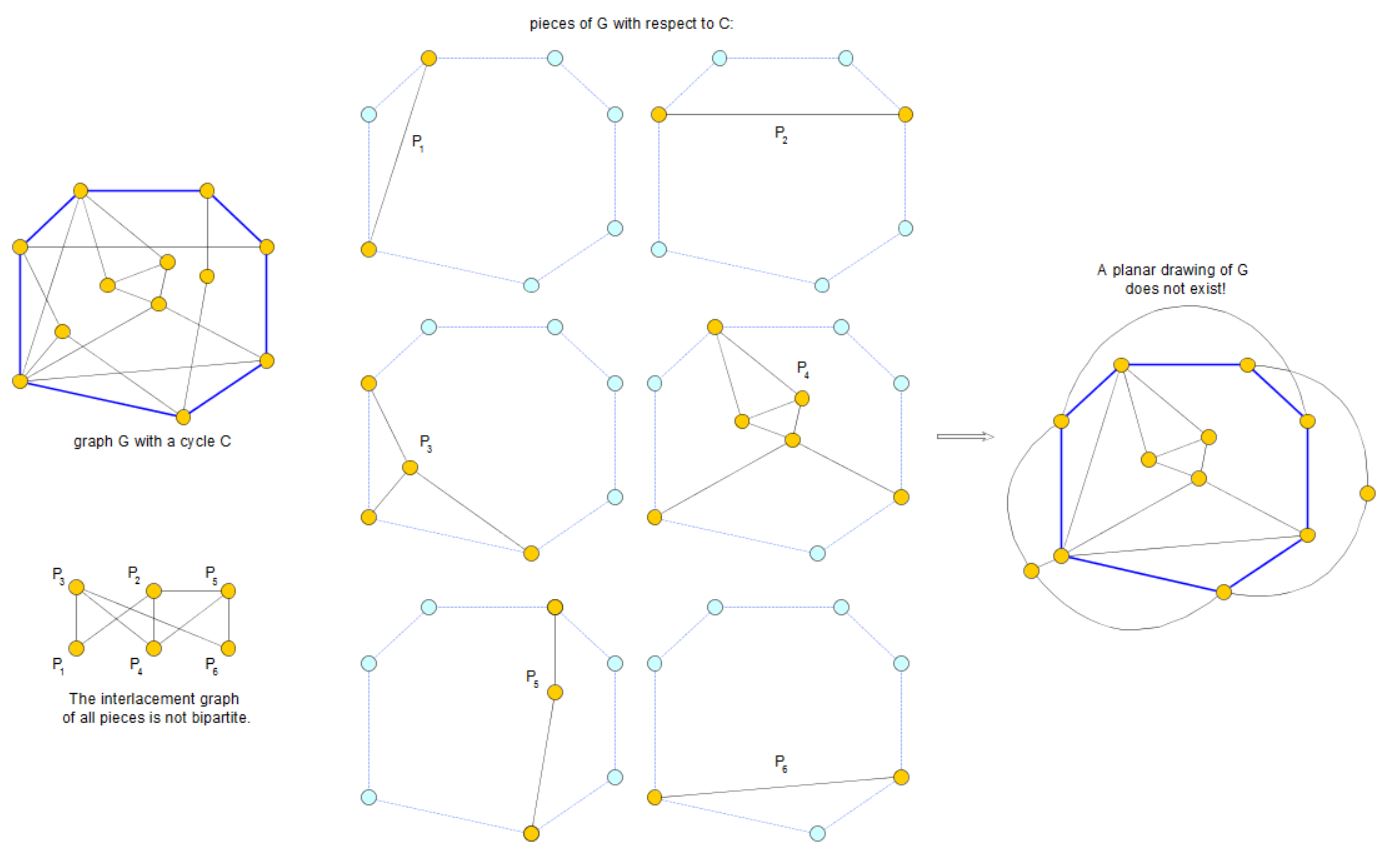
In the following figure, the graph \(G\) has been slightly changed (see piece \(P_2\)). The resulting interlacement graph is not bipartite. Although all pieces, by themselves, are planar, the graph \(G\) as a whole, is not planar. On the right side of the figure, a drawing is shown, in which the pieces \(P_2\) and \(P_5\) cross each other. The theorem proves that there is no way to find a planar drawing of \(G\).
Proofs: 1
Please note that in a biconnected graph such a cycle always exists. ↩