An undirected graph or graph \(G\) is a triple \(G:=(V,E,\gamma)\) with the following properties:
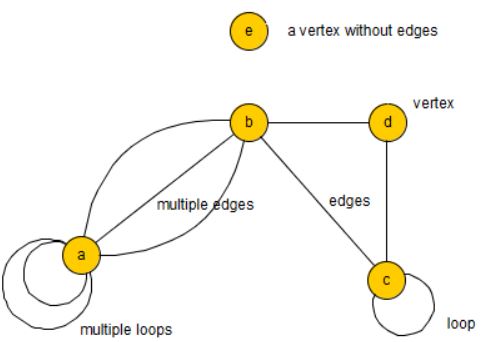
Please note that the ends of an edge \(e\) can be two different vertices (this is the case if \(|\gamma(e)|=2\)) or one an the same vertex (this is the case if \(|\gamma(e)|=1\)).
If \(|\gamma(e)|=1\), i.e. if the ends of \(e\) are the same vertex, the edge \(e\) is called a loop.
Two edges \(e\) and \(e'\) are called parallel or multiple edges if \(\gamma(e)=\gamma(e')\), (thus they have the same ends). If additionally \(|\gamma(e)|=1\), they are called multiple loops.
We call \(G\) a simple undirected graph (or simple graph), if it has no loops and no parallel edges. A simple graph is written \(G(V,E)\). An edge of simple graph \(e:=(x,y)\) is written as \(xy\) (or \(yx\)).
Algorithms: 1 2 3
Chapters: 4
Corollaries: 5 6
Definitions: 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Examples: 46
Explanations: 47
Lemmas: 48 49 50 51 52 53
Motivations: 54
Persons: 55
Proofs: 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
Propositions: 76 77 78 79 80
Theorems: 81 82 83 84 85 86 87 88 89 90 91