◀ ▲ ▶Branches / Graph-theory / Definition: Root, Degree of a Tree, Subtree, Height

Definition: Root, Degree of a Tree, Subtree, Height

Let a tree $T$ be given and let $r$ be a designated vertex of that tree called its root. * The subtrees of $T$ (with respect to the root $r$) are the disconnected subgraphs of $T$ when disconnected by removing the root $r.$ * The roots of the subtrees are those uniquely determined vertices, which were adjacent to $r$ before it was removed. * The degree of $T$ (with respect to the root $r$) is the maximum vertex degree of its root and all vertex degrees of roots of its subtrees obtained recursively by removing their roots. * The height of $T$ (with respect to the root $r$) is the maximum length of a path between $r$ and its leaves.

Example

The following figure demonstrates the above concepts and also the fact that they indeed depend on the special choice of the root. You see the same tree drawn in two different ways.

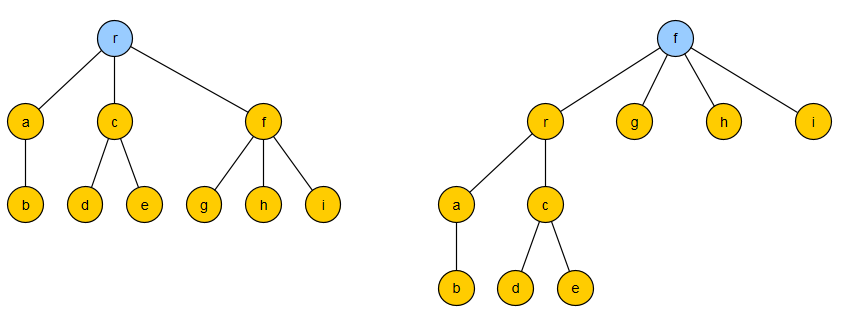
In the left drawing:

• $r$ is the root.
• The induced graphs $G[a,b]$, $G[c,d,e]$ and $G[f,g,h,j]$ are subtrees with their respective roots $a$, $c$ and $f.$
• After a recursive removal of these roots, we get the graphs $G[b]$, $G[d]$, $G[e]$, $G[g]$, $G[h]$, and $G[i]$, which are their own roots, have no more subtrees, and, at the same time, are the leafs of the original tree.
• The maximum degree of all consecutive roots is $3,$ thus the order of this tree is $3.$
• The height of the tree is $2.$

In the right drawing:

• $f$ is the root.
• The induced graphs $G[r,a,b,c,d,e],$ $G[g]$, $G[h]$, $G[i]$ are subtrees with their respective roots $r$, $g$, $h$ and $i$.
• Only $G[r,a,b,c,d,e]$ has two subtrees $G[a,b]$, $G[c,d,e]$.
• After a recursive removal of their roots $a$ and $c$, we get the graphs $G[b]$, $G[d]$, $G[e]$, which are their own roots and have no more subtrees.
• The maximum degree of all consecutive roots is now $4.$ Thus, the order of this tree is $4.$
• The height of the tree is $3.$

Mentioned in:

Definitions: 1
Lemmas: 2
Proofs: 3

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Krumke S. O., Noltemeier H.: "Graphentheoretische Konzepte und Algorithmen", Teubner, 2005, 1st Edition