Definition: Subgraphs and Supergraphs; Induced Subgraph

Let \(G(V,E,\gamma)\) be an undirected graph. A graph \(S(V',E',\gamma')\) is called a subgraph of \(G\), written as \(S\subseteq G\), if it fulfills the following properties:

\(V'\) consists only of vertices from \(V\), formally \(V'\subseteq V\).
\(E'\) consists only of edges from \(E\), formally \(E'\subseteq E\).
\(\gamma'\) is the restriction of \(\gamma\) on \(E'\), i.e. \(\gamma':={\gamma|}_{E'}E\mapsto V\). (Note: This property is not necessary for a simple undirected graph \(G(V,E)\)).

If \(S\) is a subgraph of \(G\), then \(G\) is called the supergraph of \(S\).

If \(S\) contains all the edges \(e\) with \(\gamma(e)\in V'\), then \(S\) is an induced subgraph of \(G\); we say that the vertices \(V'\) induce or span \(S\) in \(G\) and write \(S:=G[V']\). Thus, if \(V'\subseteq V\) is any set of vertices, \(V'=\{v_1,v_2,\ldots,v_n\}\), then the induced subgraph \(G[V']=G[v_1,v_2,\ldots,v_n]\) denotes the graph whose edges are precisely the edges of \(G\) with ends in \(V'\).

Example

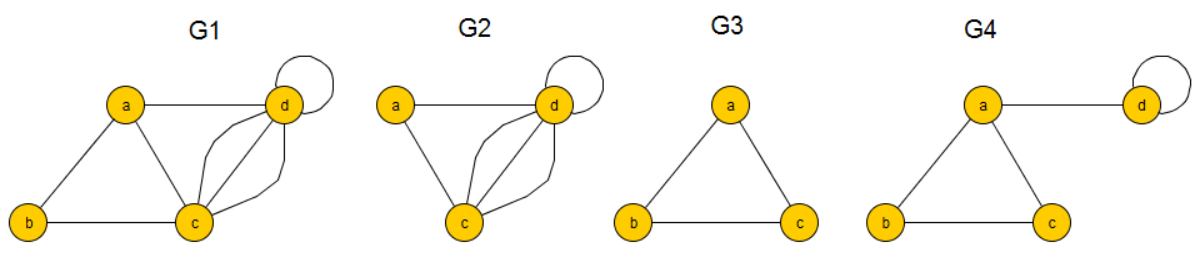
inducedgraph

In the above figure, the graphs \(G_2, G_3\) and \(G_4\) are all subgraphs of the graph \(G_1\). However, only \(G_2\) and \(G_3\) are induced subgraphs of \(G_1\), since

\[G_2=G_1[a,c,d],\quad G_3=G_1[a,b,c],\]

but

\[G_4\neq G_1[a,b,c,d].\]