◀ ▲ ▶Branches / Graph-theory / Definition: Separating and Non-Separating Cycles

Definition: Separating and Non-Separating Cycles

Let \(G(V,E,\gamma)\) be an biconnected graph and let \(C(V_c,E_c)\) be a cycle in \(G\)¹.

\(C\) is called separating if there are at least two pieces of \(G\) with respect to \(C\) . \(C\) is called non-separating if there only one piece of \(G\) with respect to \(C\) .

Example

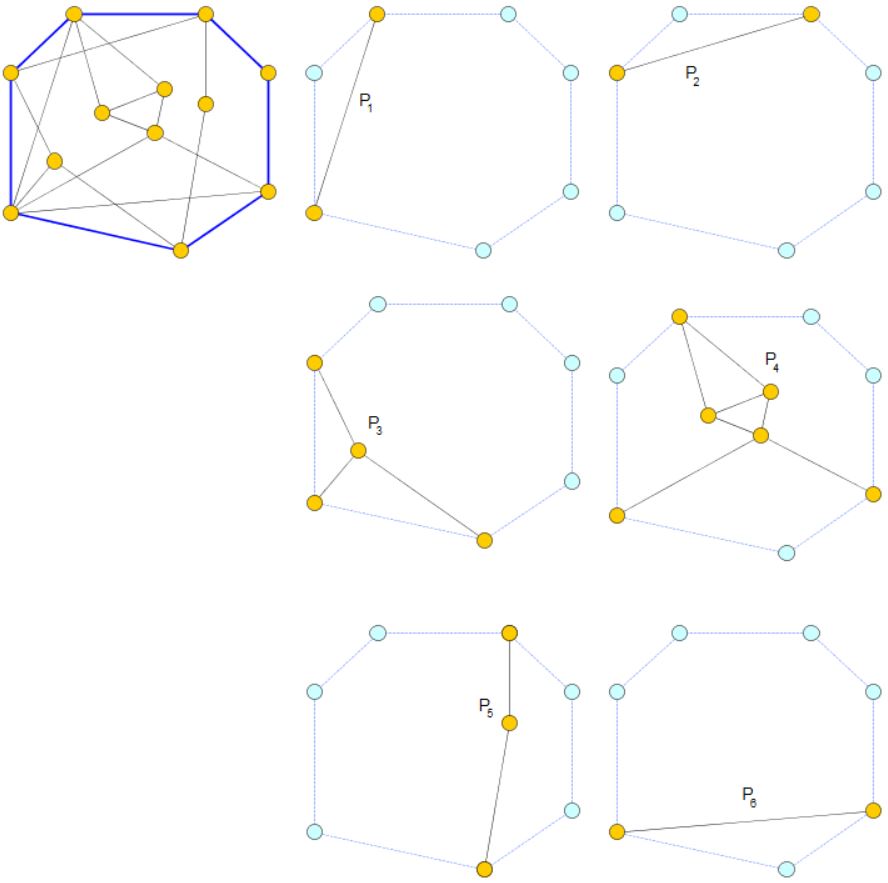
In the following graph, the cycle (blue) is non-separating, since it has only one piece \(P\) (highlighted orange on the right).

Another cycle in the same graph (also marked blue) is separating, since it has \(6\) pieces \(P_1,P_2,\ldots,P_6\) (highlighted orange on the right):

Mentioned in:

Lemmas: 1
Proofs: 2

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Di Battista G., Eades P., Tamassia R., Tollis, I.G.: "Graph Drawing - Algorithms for the Visualization of Graphs", Prentice-Hall, Inc., 1999

Footnotes