(related to Lemma: When is it possible to find a separating cycle in a biconnected graph, given a non-separating cycle?)
Let \(G(V,E,\gamma)\) be a biconnected graph and let \(C(V_c,E_c)\) be a non-separating cycle with the piece \(P(V_p,E_p)\), which is, by hypothesis, not a path. Let \(u\) and \(v\) be two attachments of \(P\) that are consecutive in the circular order of \(C\), i.e. if \(C:=x_0x_1\ldots x_{k-1}x_k\) with \(x_k=x_0\), then \(u=x_i\) and \(v=x_j\) for some \( i < j\) and there is no other attachment of \(P\) among the vertices \(u=x_i,x_{i+1},\ldots,x_{j-1},x_j=v\), besides \(u\) and \(v\).
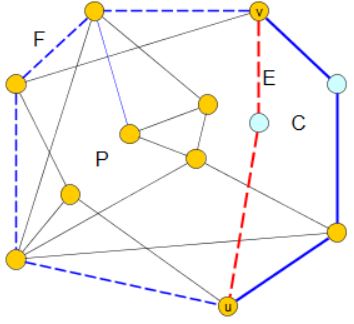
In the example below, the edges of the cycle \(C\) are colored blue and the vertices of the piece \(P\) are colored orange. Moreover, \(u\) and \(v\) are two attachments of \(P\) that are consecutive in the circular order of \(C\):

We want to show that, provided \(P\) is not a path (which is the case in our example), it is possible to construct a separating cycle \(S(V_s,E_s)\), which consists of a subpath of \(C\) plus a path of \(P\) between the attachments \(u\) and \(v\) of \(P\).
We observe that, by construction, \(E=x_ix_{i+1}\ldots x_{j-1}x_j\) is a subpath of \(C\) from \(u\) to \(v\) that does not contain any attachment of \(P\). Moreover, by definition of a piece, \(P(V_p,E_p)\) is connected. Thus, there is also another path \(F\) from \(u\) to \(v\) in \(P\).
In our example, both paths \(E\) (dashed red) and \(F\) (dashed blue) are shown in the following figure:
Let \(S\) be a cycle obtained from \(C\) by replacing \(E\) with \(F\) (see next figure):
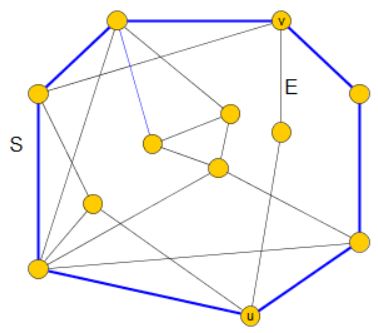
It remains to be shown that \(S\) is a separating cycle cycle. First of all, we have by construction that \(E\) is a piece of \(G\) with respect to \(S\). By hypothesis, \(P\) is not a path. Therefore, there exists an edge \(e\) of \(P\) which is not an edge of \(F\). Therefore, there must exist another piece of \(G\) with respect to \(S\), which is distinct to \(E\) (see next figure):
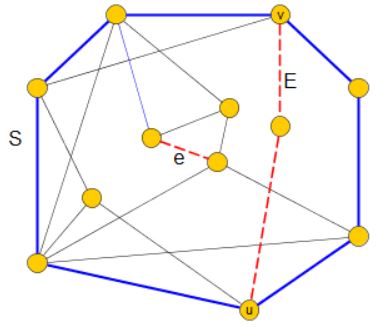
Since there are more than one pieces of \(G\) with respect to \(S\), \(S\) is a separating cycle.