Let \(G(V,E,\gamma)\) be an biconnected graph and let \(C(V_c,E_c)\) be a cycle in \(G\)1, such that the cycle \(C\) (but not necessarily the whole graph \(G\)) has2 a planar drawing so that the planar drawing of \(C\) divides the plane into an interior region bounded by the drawing and an exterior region3.
In the following figure a drawing of a graph \(G\) is shown, which is not planar, however, the cycle \(C\) (blue) has a planar drawing:

We say that two pieces of \(G\) with respect to \(C\) interlace, if they can neither be drawn entirely in the interior of \(C\) nor can they be drawn entirely in the exterior of \(C\), without violating planarity.
In our example, there are \(6\) pieces of \(G\) with respect to \(C\). In particular, the pieces \(P_2\) and \(P_1\) interlace, while the the pieces \(P_2\) and \(P_3\) do not interlace:
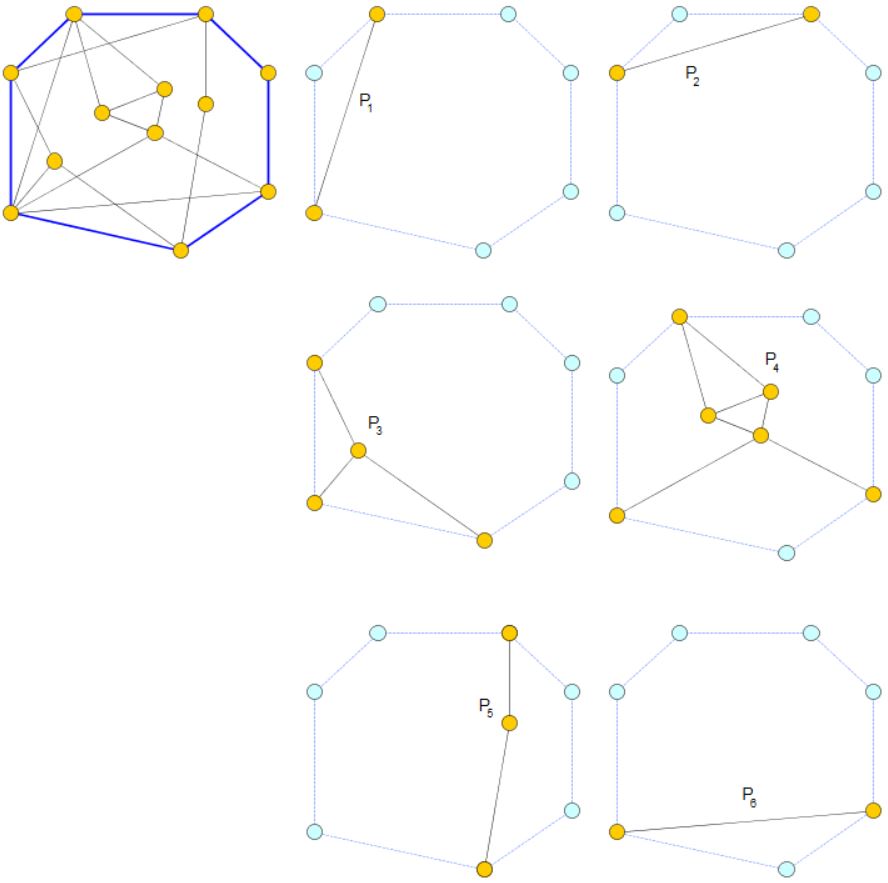
The interlacement graph \(I(V_i,E_i)\) of the pieces of \(G\) with respect to \(C\) is the graph whose vertices \(V_i\) are the pieces of \(G\) and whose edges \(E_i\) are the pairs of pieces that interlace.
The following figure demonstrates the interlacement graph of our example:
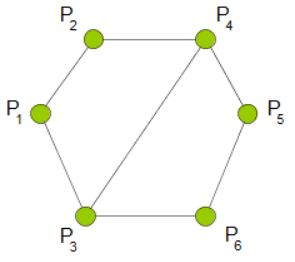
Theorems: 1
Please note that in a biconnected graph such a cycle always exists. ↩
Please note that every cycle has a planar drawing. The condition requiring \(C\) to have a planar drawing is made in this definition only for the reason to make sure that an interior and exterior of the drawing of \(C\) exists. ↩
The existence of an interior and an exterior region follows from the Jordan Curve Theorem (still to be done at BookOfProofs). ↩