Definition: Pieces of a Graph With Respect to A Cycle

Let \(G(V,E,\gamma)\) be an biconnected graph and let \(C(V_c,E_c)\) be a cycle in \(G\)¹. The cycle \(C\) partitions all edges \(E\setminus E_c\), i.e. the edges, which are not in the cycle, into equivalence classes in the following way:

Two edges \(e_1,e_2\in E\setminus E_c\) are equivalent if and only if there is a path \(P(V_p,E_p)\) between them that does not contain any vertex of \(C\), formally \[\forall e_1,e_2\in E\setminus E_c:~e_1\equiv e_2\Longleftrightarrow\exists \text{ path }P:~e_1,e_2\in E_p\wedge V_p\cap V_c=\emptyset.\]

The subgraphs of \(G\) induced by these equivalence classes are called the pieces of the graph \(G\) with respect to the cycle \(C\).

The vertices of a piece \(P_i(V_i,E_i)\) with respect to the cycle \(C(V_c,E_c)\) that are also in \(C\), i.e. \(v\in V_i\cap V_c\), are called the attachments of that piece.

Example

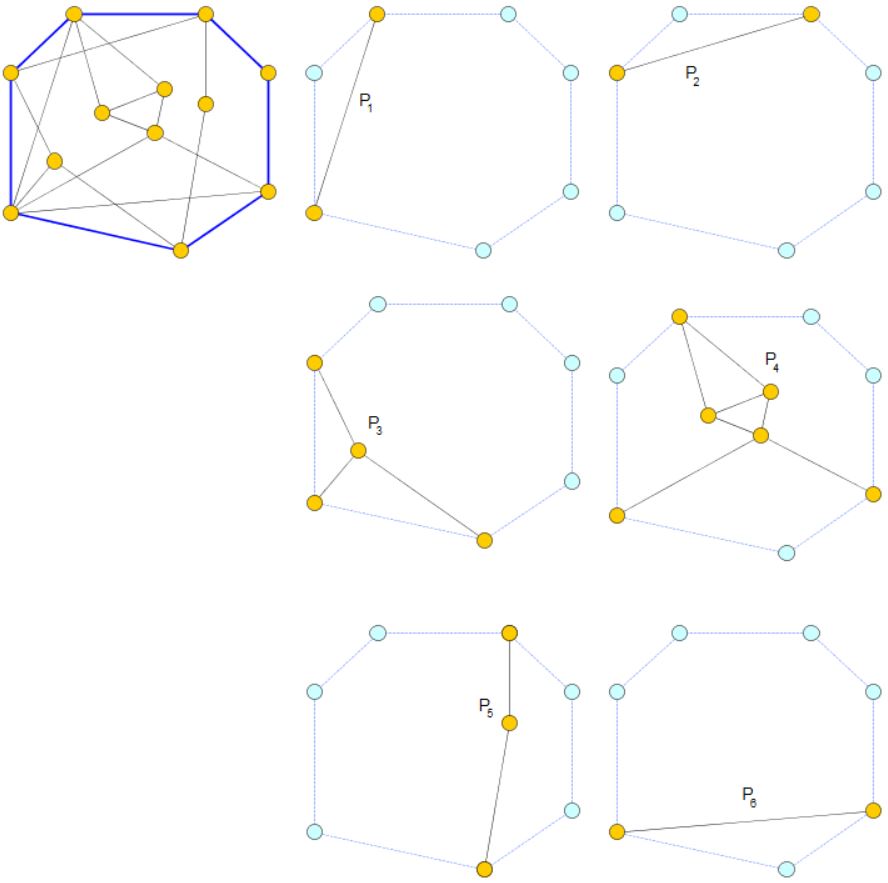
A graph (left-upper corner) with a cycle (blue) and the corresponding partition of this graph into \(6\) pieces \(P_1,P_2,\ldots,P_6\). While \(P_1,P_2,P_5,P_6\) have two attachments, the pieces \(P_3\) and \(P_4\) have three attachments.

pieces