The complex conjugate of a complex number is its reflection on the real axis in the complex plane.
Let \(z=x + yi\in\mathbb C\) be a complex number. The complex conjugate of \(z\), denoted by \(z^* \), is the complex number with the same real part and the negative imaginary part, i.e.
\[z^* :=\Re(z) - \Im (z) i=x - y i.\]
In the complex plane, complex conjugates can be interpreted as the reflections of complex numbers across the real axis, as shown in the below figure
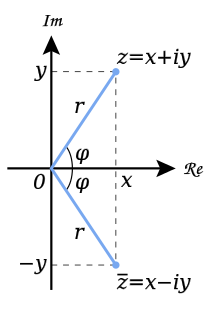
(from Wikipedia, uploaded by Aflafla1)
Below, you can experiment with complex conjugation of a polygon in the complex plane. Just move around (e.g. using your mouse, mouse-pad or touchscreen) the points in the \(z\)-Plane and see the result in the \(w\)-Plane:
\(z\)-Plane:
\(w\)-Plane with \(w:= z^\ast \):
Corollaries: 1
Definitions: 2 3 4
Examples: 5
Proofs: 6 7 8 9 10 11 12
Propositions: 13 14 15 16