The existence of a singleton $\{X\}$ for every set $X$ raises the question if both are equal. If we take the definition of set equality as a basis, then we must ask ourselves if $X\subseteq \{X\}$ and if $\{X\}\subseteq X$. Certainly, $X\in \{X\}$ by definition of the singleton, and, using the axiom of separation, we can separate this element to get a subset containing the element $X$ which is a subset of the initial singleton $\{X\}.$ But this subset is again a singleton of $X$, by construction, and we get the trivial result $\{X\}\subseteq \{X\}$. By symmetry, we also get $\{X\}\supseteq \{X\}$ and we only get the trivial result $\{X\}=\{X\}.$
Another approach to decide, if $X=\{X\}$ would be to assume this and check if this assumption leads to a contradiction. Let us try. Assume $X=\{X\}$. Since $X\in \{X\}$, we get $X\in X,$ i.e. a set containing itself. Please note that even with the axiom of extensionality we cannot decide, if such a set can exist. Obviously, if such a set existed, then we would allow never-ending chains $\ldots\in X\in X\in\ldots\in X\in\ldots$ or circular referencec, like for instance in the following chain $X\in X_1\in X_2\in X.$
Therefore, we have to determine, if we want to allow such constructions in our set theory or not. The additional axiom of foundation forbids such constructions. It was added to the original set of axioms of Zermelo by Fraenkel and von Neumann and helps to avoid paradoxes mentioned in the historical development of the set theory, which threw mathematics in a fundamental crisis at the beginning of the 20th century.
Every non-empty set \(X\) contains an element that is disjoint from \(X\). This can be formalized as
\[\forall X(X\neq\emptyset \Rightarrow\exists z(z\in X \wedge X\cap z=\emptyset)).\]
Note: The following figure demonstrates this axiom for the singleton:
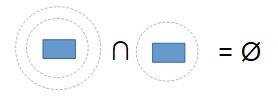
and makes sure that $X\neq \{X\}$ for all sets $X.$
Corollaries: 1
Axioms: 1
Definitions: 2
Examples: 3 4
Motivations: 5
Proofs: 6 7 8 9 10 11 12 13