◀ ▲ ▶Branches / Set-theory / Definition: Singleton

We have just shown how the axiom of power set ensures the existence and uniqueness of the power set. The following diagram illustrates the power set $\mathcal P(X)$ for a set $X$ containing three elements:

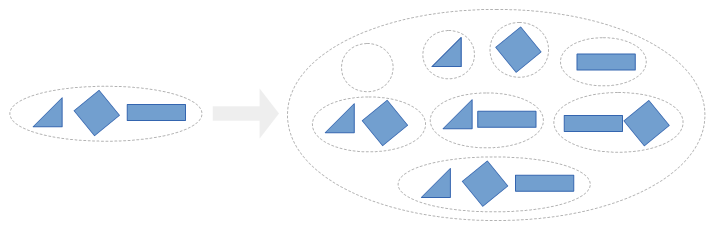
Using the axiom of separation, we can now separate a subset of $\mathcal P(X)$ containing exactly $X$ as its single element:

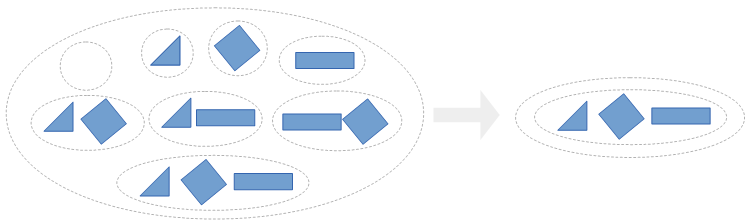
Moreover, the resulting set is unique by the axiom of extensionality. This motivates the following definition:

Definition: Singleton

For every set $X$ the set $\{X\}$ is well-defined and is called the singleton of $X.$ Formally, using the power set, we have $$\{X\}:=\{z\in\mathcal P(X)\mid z=X\}.$$

Mentioned in:

Applications: 1
Axioms: 2
Definitions: 3
Examples: 4 5
Proofs: 6 7 8 9 10 11 12
Propositions: 13

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Hoffmann, Dirk W.: "Grenzen der Mathematik - Eine Reise durch die Kerngebiete der mathematischen Logik", Spektrum Akademischer Verlag, 2011
2. Ebbinghaus, H.-D.: "Einführung in die Mengenlehre", BI Wisschenschaftsverlag, 1994, 3th Edition