◀ ▲ ▶Branches / Set-theory / Axiom: Axiom of Extensionality

Axiom: Axiom of Extensionality

If each element of the set \(X\) is also an element of the set \(Y\) and vice versa, then both are the same. In other words, a set is determined by its elements¹, which is known as the extensionality principle.

\[\forall X~\forall Y (\forall z~(z\in X \Leftrightarrow z\in Y)\Rightarrow X=Y)\]

Table of Contents

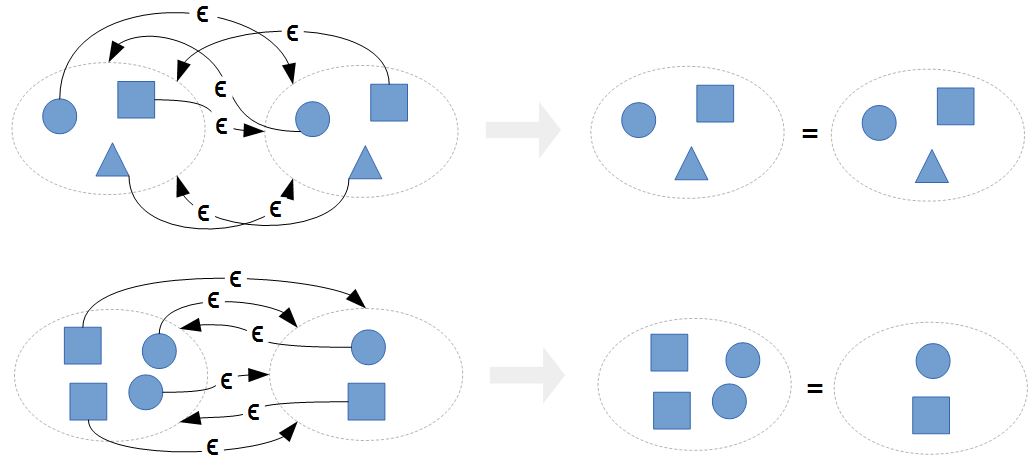
Explanations: 1

Mentioned in:

Axioms: 1 2 3 4
Corollaries: 5
Definitions: 6
Explanations: 7
Parts: 8
Proofs: 9 10 11 12 13 14 15 16 17 18 19

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Hoffmann, Dirk W.: "Grenzen der Mathematik - Eine Reise durch die Kerngebiete der mathematischen Logik", Spektrum Akademischer Verlag, 2011
2. Wille, D; Holz, M: "Repetitorium der Linearen Algebra", Binomi Verlag, 1994

Footnotes