◀ ▲ ▶Branches / Set-theory / Definition: Set Complement

Definition: Set Complement

Let $X$ and $A$ be sets. Based on the conjunction "\(\wedge\)", and the negation "\(\neg\)", the complement of the subset \(A\subseteq X\) is defined by

\[A^C :=\{x \mid x\in X\wedge x\notin A\}.\]

In particular, $A^C\subseteq X.$ Thus, for a subset $A\subseteq X$, The complement $A^C$ contains all elements \(x\) of \(X\), which are not contained in \(A\).

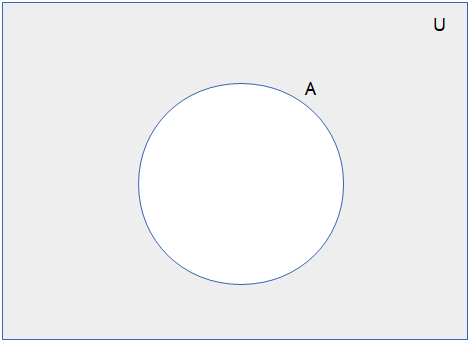
A set complement can be drawn in a Venn diagram using its universal set as follows:

Examples:

1. The complement of the even numbers in the universal set of all whole numbers are the odd numbers.
2. The complement of the even numbers in the universal set of all whole numbers are the odd numbers.

Mentioned in:

Corollaries: 1
Definitions: 2 3
Explanations: 4
Proofs: 5 6 7 8 9 10 11 12
Propositions: 13 14

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Reinhardt F., Soeder H.: "dtv-Atlas zur Mathematik", Deutsche Taschenbuch Verlag, 1994, 10th Edition
2. Kohar, Richard: "Basic Discrete Mathematics, Logic, Set Theory & Probability", World Scientific, 2016