◀ ▲ ▶Branches / Theoretical-computer-science / Formal-languages / Application: Application of the Theorem to Reduce `$\epsilon$`-NFA to NFA

Application: Application of the Theorem to Reduce $\epsilon$-NFA to NFA

(related to Chapter: Finite Automata (Finite Sequential Machines))

The following are examples to apply the construction given in the proof of the theorem about the reduction of $\epsilon$-NFA to NFA, reducing the examples of $\epsilon$-NFA to the corresponding NFA.

Ad Example $(2)$

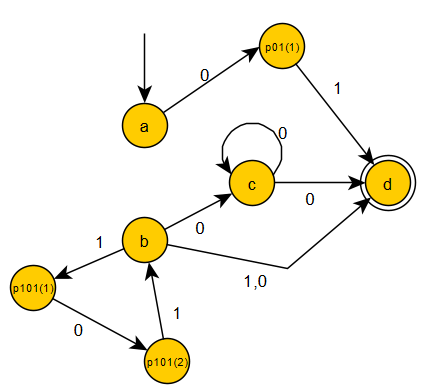
Please note that in this example, the intermediate states $p_{01}(1), p_{101}(1)$ and $p_{101}(2)$ have been added to reflect transitions marked by words with length $\ge 2$ in the original graph of the second $\epsilon$-NFA example. Also, the original $\epsilon$ transition from the state $a$ to the state $b$ disappeared, since there is no predecessor state $t$ and symbol $x\in\{0,1\}$ such that $\Delta^\prime(t,x)=a.$

Ad Example $(3)$

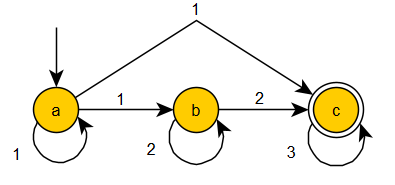
In this example, no new intermediate states are needed to reduce the original $\epsilon$-NFA to an NFA. However, we have to deal with the original $\epsilon$ transitions between the states $a\to b$ and $b\to c$ and replace them according to the construction in the proofproof/. The construction steps are as follows:

1. We first take over all loop transitions $a\to a$ via $1$, $b\to b$ via $2$ and $c\to c$ via $3$. Those remain unchanged since they use words of length $1.$
2. Dealing with $a\to b$ via the empty word $\epsilon$ in the original graph: There is only one predecessor transition of $a$ in the new graph, namely $\Delta^\prime(a,1)=a.$ Therefore, we add $\Delta^\prime(a,1)=b.$
3. Dealing with $a\to b$ via the empty word $\epsilon$ in the original graph: There is only one predecessor transition of $a$ in the new graph, namely $\Delta^\prime(a,1)=a.$ Therefore, we add $\Delta^\prime(a,1)=b.$

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Erk, Katrin; Priese, Lutz: "Theoretische Informatik", Springer Verlag, 2000, 2nd Edition
2. Hoffmann, Dirk: "Theoretische Informatik, 3. Auflage", Hanser, 2015