Branches History Index

◀ ▲ ▶Branches / Theoretical-computer-science / Formal-languages / Application: Application of the Rabin-Scott Theorem - the Rabin-Scott Algorithm

Application: Application of the Rabin-Scott Theorem - the Rabin-Scott Algorithm

(related to Chapter: Finite Automata (Finite Sequential Machines))

As an application of the Rabin-Scott Theorem we can design the following algorithm to change any given NFA $(C,\Sigma,\Delta,F,s_0)$ to a corresponding DFA $(C^\prime,\Sigma,\delta,F^\prime,s_0^\prime)$.

  1. Label in a table all columns with the symbols in the alphabet $\Sigma$.
  2. Set $i=0$.
  3. Label the $0$-th row of the table with the singleton $\{s_0\}$ of the starting state $s_0$.
  4. Fill in the $i$-th row with the label $s_i^\prime$ for each symbol $\sigma\in \Sigma$ (column label) exactly the subset $Q\subseteq C$ of states which can be reached in the NFA by applying $\Delta$ to the pair $(s_i^\prime,\sigma)$
  5. Add as many new rows to the table, as there are new subsets $Q\in C$ found in the previous row and label them with these subsets. Increment $i$ by the number of rows added.
  6. Repeat the procedure from step 4, until no more new subsets $Q\in C$ are found.
  7. Draw the diagram of the DFA accordingly, mark $\{s_0\}$ as the starting state and those states $s_i^\prime$ as final states of the DFA, which contain at least one final state of the NFA.

We want to apply this algorithm to one of the NFA shown in the examples of NFA:

nfa2

This NFA accepts the language $L=\{10,101\}^*$. The table created by the algorithm is this:

$$\begin{array}{c|c|c|c} i&s_i^\prime&1&0\\ \hline 0&\{a\}&\{b\}&\{\emptyset\}\\ 1&\{b\}&\{\emptyset\}&\{a,c\}\\ 2&\{\emptyset\}&\{\emptyset\}&\{\emptyset\}\\ 3&\{a,c\}&\{a,b\}&\{\emptyset\}\\ 4&\{a,b\}&\{b\}&\{a,c\}\\ \end{array}$$

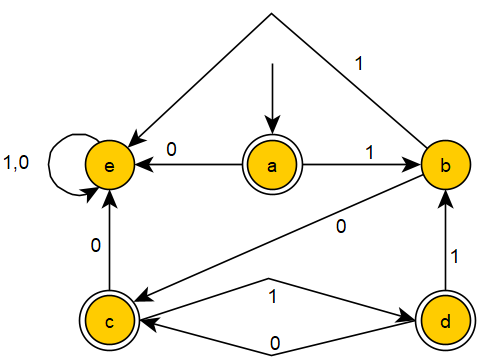
It is now clear that the rows of the table are labeled by the states of the constructed DFA. The number of these rows cannot (by the Rabin-Scott theorem) exceed $2^3=8$, which is the number of elements of the power set of the set of the states $\{a,b,c\}$ of the given NFA. The resulting DFA can be drawn as

dfa7

Finally, we can re-label the nodes to make the drawing more concise, and we are done. We have found a DFA accepting exactly the same language as the given NFA.

dfa6

Rabin and Scott were honored 1976 for their paper with the Turing award. They demonstrated that NFA and DFA provide an efficient model for the study of formal languages. Moreover, they stimulated the theoretical computer science by their ideas of determinism and non-determinism of finite automata. They wrote:

"A nondeterministic automaton is not a probabilistic machine but rather a machine with many choices in its moves. At each stage of its motion across a tape it will be at liberty to choose one of several new internal states. Of course, some sequence of choices will lead either to impossible situations from which no moves are possible or to final states not in the designated class $F.$ We disregard all such failures, however, and agree to let the machine accept a tape if there is at least one winning combination of choices of states leading to a designated final state."

Thank you to the contributors under CC BY-SA 4.0!

Github:
bookofproofs

References

Bibliography

  1. Erk, Katrin; Priese, Lutz: "Theoretische Informatik", Springer Verlag, 2000, 2nd Edition
  2. Hoffmann, Dirk: "Theoretische Informatik, 3. Auflage", Hanser, 2015