Many technical machines (for instance an ATM) have a different number of states (e.g. off, idle, customer authentication, selecting transaction, transaction, out of service, etc.) and their complexity grows with the growing number of states. Finite automata are models helping to systematically describe such systems. These can be technical systems and machines (like an ATM), but, surprisingly, we can also use finite automata to solve theoretical problems in conjunction with formal languages, which will be shown to be very good models of computation.
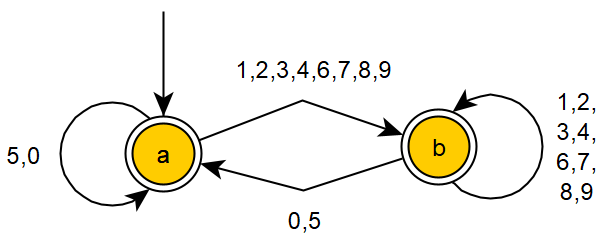
The following example illustrates the concept of a finite automaton. The example has two states $a$ and $b$. The state $a$ is the starting state (denoted by an incoming arrow $\downarrow$). At the same time, the states $a$ and $b$ are end states (denoted by double circles). The automaton accepts strings which are decimal numbers, reads them digit by digit from left to right and ends at the state $a$ if and only if the number is divisible by $5$, otherwise the end state will be $b$.
In this section, we will learn about different types of finite automata (FA), including: * FA without an output (so-called acceptors): * DFA - deterministic finite automata * NFA - non-deterministic finite automata * $\epsilon$-NFA - $\epsilon$ non-deterministic automata * FA with output (so-called transducers): * Moore Machine * Mealy Machine
Applications: 1 2 Examples: 1 2 3