(related to Chapter: Finite Automata (Finite Sequential Machines))
This DFA accepts words over the alphabet $\{0,1,2,3,4,5,6,7,8,9\}$ and decides whether or not they denote a positive integer divisible by $5$.
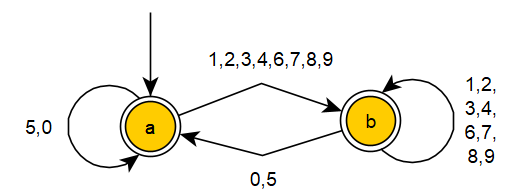
For instance, the input word $19403$ will lead to the states $abbbab$, and the end state $b$ shows that $19403$ is not divisible by $5$. The input word $925$ will lead to the states $abba$, and the end state $a$ shows that $925$ is divisible by $5$.
This DFA accepts words over the alphabet $\{0,1\}$ with exactly two $1$'s.
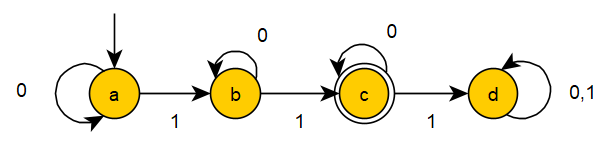
If a string has more than two $1$'s, the DFA will enter the state $d$ which is not demarked as final.
This DFA accepts words from the alphabet $\{0,1\}$ containing an even number of $1$'s.
