(related to Chapter: Finite Automata (Finite Sequential Machines))
Non-deterministic finite automata can be illustrated using diagrams like it was the case for the DFA.
Please note that the NFA definition is more general than the DFA definition since it replaces a function $\delta$ by a relation $\Delta$ (every function is a relation but not every relation is a function).
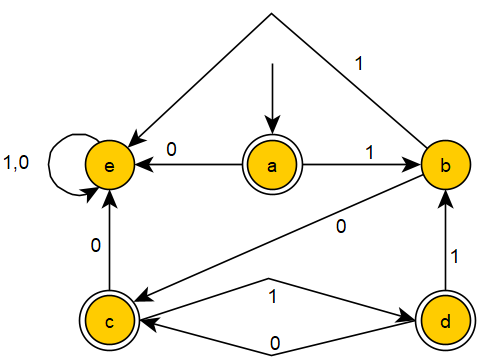
The following example of an NFA accepts all strings over the alphabet $\{0,1\}$ whose second to the last symbol is $1.$
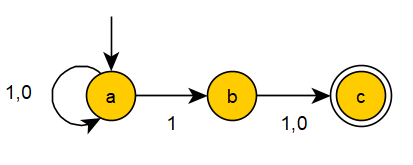
Note that the same strings can be accepted by this, more complex, DFA:
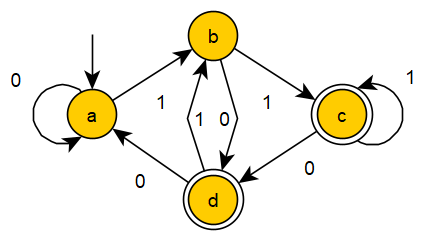
The following example of an NFA accepts all strings over the alphabet $\{0,1\}$ that are concatenations of $10$ and $101$. In other words, the language accepted by the NFA is $\{10,101\}^*$:

As in example 2, the same strings can be accepted by another, much more complex, DFA: