Proposition: 7.20: Ratios of Fractions in Lowest Terms

Euclid's Formulation

The least numbers of those (numbers) having the same ratio measure those (numbers) having the same ratio as them an equal number of times, the greater (measuring) the greater, and the lesser the lesser.

For let $CD$ and $EF$ be the least numbers having the same ratio as $A$ and $B$ (respectively).
I say that $CD$ measures $A$ the same number of times as $EF$ (measures) $B$.

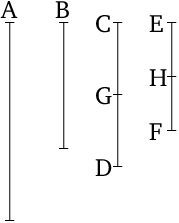
fig20e

Modern Formulation

If $\frac{\overline{CD}}{\overline{EF}}=\frac{A}{B}$ (all lengths being natural numbers) and $\frac{\overline{CD}}{\overline{EF}}$ is a reduced fraction, i.e. $\overline{CD}$ and $\overline{EF}$ are co-prime, then there exists a natural number $n$ such that $A=n\cdot \overline{CD}$ and $B=n\cdot \overline{EF}.$ In other words, the ratio $\frac AB$ can be reduced by the number $n.$

Proofs: 1

Proofs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15