The set of natural numbers \(\mathbb N\) is defined using the concept ordinals, as follows:
(1) The empty set (as the first ordinal)1 represents the first natural number:
\[0:=\{\emptyset\}.\]

(2) Once we have the ordinal \(n=\alpha\), we can construct a bigger ordinal2 using recursively the formula for constructing successors of ordinals, denoting the successor \(n^+\) of the natural number \(n\): \[n^+:=s(\alpha):=\alpha\cup\{\alpha\}=n\cup \{n\}.\] Applying the set axioms and this construction systematically, it gives us a chain of ordered ordinals
\[\begin{array}{rcl}0&:=&\emptyset,\\1&:=&0\cup\{0\}=\emptyset\cup\{\emptyset\}=\{\emptyset\},\\2&:=&1\cup\{1\}=\{\emptyset\}\cup\{\{\emptyset\}\}=\{\emptyset,\{\emptyset\}\},\\3&:=&2\cup\{2\}=\{\emptyset,\{\emptyset\}\}\cup\{\{\emptyset,\{\emptyset\}\}\}=\{\emptyset,\{\emptyset\},\{\emptyset,\{\emptyset\}\}\},\\&\vdots&\\n^+&:=&n\cup\{n\},\\&\vdots&\end{array}\]
which can be visualized in the following figure
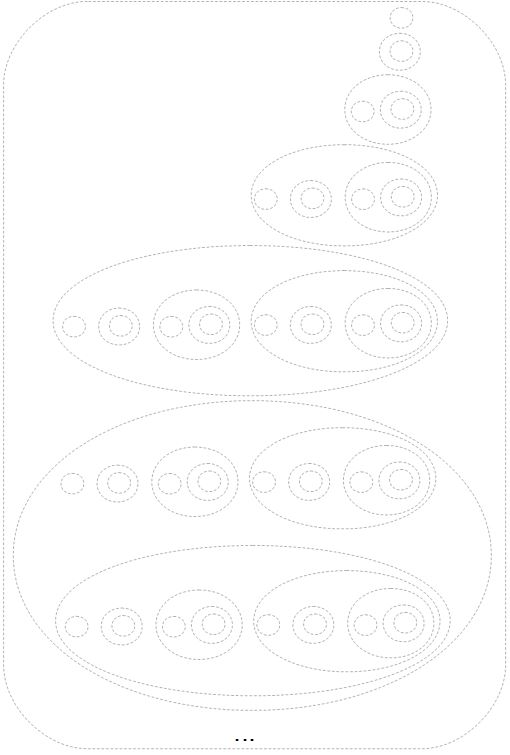
and for which we introduce the notation \(0,1,2,3,\ldots\):
\[0 < 1 < 2 < 3 < \ldots\]
Due to the axiom of infinity we can postulate the existence of an infinite set, which is "contains" all such sets.3
\[\mathbb N:=\bigcup n=\{0,1,2,3,\ldots.\}\]
The set \(\mathbb N\) of natural numbers is defined recursively by: \[\begin{array}{rcl}0&:=&\emptyset,\\1&:=&\{0\}=\{\emptyset\},\\2&:=&\{1\}=\{\{\emptyset\}\},\\3&:=&\{2\}=\{\{\{\emptyset\}\}\},\\&\vdots&\\n^+&:=&\{n\}=\underbrace{\{\ldots\{ }_{n+1\text{ times}}\emptyset\underbrace{\}\ldots\} }_{n+1\text{ times}},\\&\vdots&\\\end{array}\]
This definition can be visualized as follows:

Algorithms: 1 2
Axioms: 3
Chapters: 4 5 6 7 8
Corollaries: 9 10 11 12 13 14 15 16 17
Definitions: 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
Examples: 61 62 63 64 65 66 67 68 69 70
Explanations: 71 72 73 74 75 76
Lemmas: 77 78 79
Motivations: 80
Parts: 81 82 83 84 85
Proofs: 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157
Propositions: 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212
Solutions: 213
Theorems: 214 215 216 217 218 219 220
Please note that it is well defined due to the axiom of existence of empty set. ↩
Ordinals are sets with some interesting properties, including "trichotomy":https://www.bookofproofs.org/branches/trichotomy-of-ordinals-cantor/, ensuring that all ordinals can be compared with each other by the relation \[\alpha < \beta:\Leftrightarrow \alpha\in\beta.\] For any two ordinals, and in particular for natural numbers, we can therefore always decide which one is "bigger", "smaller", or whether they are equal to each other. ↩
Please note that this infinite set is an ordinal by definition. However, we have not built by the above construction formula, i.e. it is not a successor of any "previous" ordinal. In other words, \(\mathbb N\) is the first limit ordinal. ↩