Let \(\mathbb R^2\) be an Euclidean plane and let \(a,b\in\mathbb R\), \(b > a\) be two real numbers. Furthermore, let \(I=[a,b]\) be a closed real interval. . A planar drawing (or a planar embedding) \(\mathcal D\) of an undirected graph \(G(V,E,\gamma)\) consists of
\((i)\) an injective function1 \(f:V\to \mathbb R^2,\)
\((ii)\) for each edge \(e_i\in E\), functions \(\epsilon_i: I\to \mathbb R^2\) such that: * \(\epsilon_i\) is a simple closed curve, if \(e_i\) is a loop2, * \(\epsilon_i\) is a simple curve, if \(e_i\) is not a loop3, * if \(x,y\) are the ends of the edge \(e_i\), we either have \(\epsilon_i(a)=f(x)\) and \(\epsilon_i(b)=f(y)\) or we have \(\epsilon_i(a)=f(y)\) and \(\epsilon_i(b)=f(x)\), depending on at which vertex the curve starts and at which it ends4. * The images of the restrictions of the curves \(e_i\) on the open interval \(J:=(a,b)\), i.e. the functions \({\epsilon_i|}_{J} : I \to \mathbb R^2\) are mutually exclusive5, formally \[\epsilon_i(J)\cap\epsilon_j(J)=\emptyset\quad\quad i\neq j.\]
A graph:
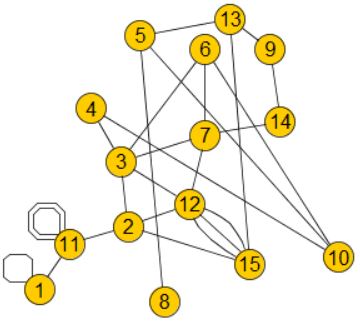
and examples of its planar drawings:
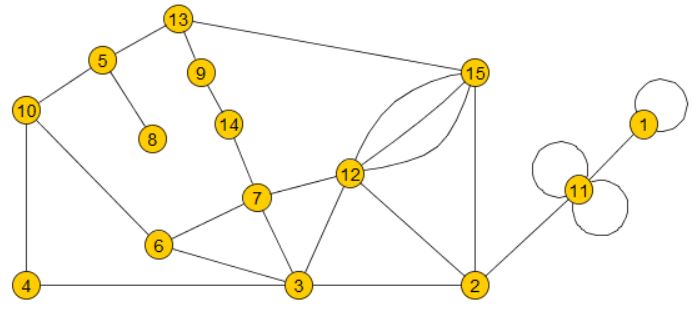

Please note that a graph can have different planar drawings.
For educational reasons, each vertex has been drawn not as a point in the plane, but as a labeled circle to enable the reader to compare all graphs.
Chapters: 1
Corollaries: 2
Definitions: 3 4 5 6 7
Lemmas: 8 9
Proofs: 10 11 12 13 14 15 16
Theorems: 17 18
The injectivity of \(f\) makes sure that \(f\) assigns to each vertex of \(G\) a unique point in the Euclidean plane \(\mathbb R^2\), i.e. the same point of the plane is never assigned to two different vertices. ↩
This property ensures that the drawing \(\epsilon_i\) of a loop does not cross itself. ↩
This property ensures that the drawing \(\epsilon_i\) of the edge does not cross itself. ↩
Please note that since \(f(x), f(y)\) are the points in the plane, which are drawings of the vertices \(x,y\), this property ensures that the drawing of any edge connecting these vertices (i.e. the curve \(\epsilon_i\)) starts (\(\epsilon_i(a)\)) and ends (\(\epsilon_i(b)\)) exactly at these points in the plane. ↩
This property makes sure that the drawings of any two edges do not cross, except at the endpoints (i.e. the vertices). ↩