◀ ▲ ▶Branches / Set-theory / Definition: Injective Function

Definition: Injective Function

A function \(f:A\mapsto B\) is called injective, (or injection, or embedding, or, less formally, one-to-one), if for all \(a_1,a_2\in A\) with $f(a_1)=f(a_2)$ it follows that $a_1=a_2.$ This corresponds to the left-unique property, in addition to the defining properties of a function.

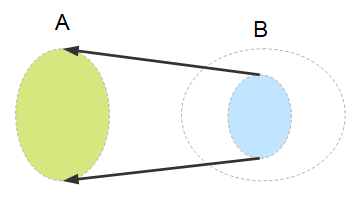
By a contraposition argument the following definition is equivalent: For all \(a_1,a_2\in A\), it follows from $a_1\neq a_2$ that $f(a_1)\neq f(a_2).$

Notes

• An injective function allows for every $b\in B$ at most an $a\in A$ such that $f(a)=b.$
• In other words, either there is exactly one or no such element $a\in A.$

Mentioned in:

Chapters: 1
Corollaries: 2
Definitions: 3 4 5 6 7 8
Explanations: 9 10
Lemmas: 11
Proofs: 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
Propositions: 32 33 34 35 36
Theorems: 37

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Knauer Ulrich: "Diskrete Strukturen - kurz gefasst", Spektrum Akademischer Verlag, 2001
2. Reinhardt F., Soeder H.: "dtv-Atlas zur Mathematik", Deutsche Taschenbuch Verlag, 1994, 10th Edition
3. Kane, Jonathan: "Writing Proofs in Analysis", Springer, 2016