The Pythagoreans believed that all magnitudes in nature could be represented the intrinsic properties of whole numbers. One should always be able to find a fundamental unit that fits some whole number of times into two different magnitudes. They called this idea the commensurabilty of these geometrical magnitudes.
In particular, the asked themselves, if a diagonal of a square (first magnitude $d$) would be commensurable with a side of the square (second magnitude $a$):
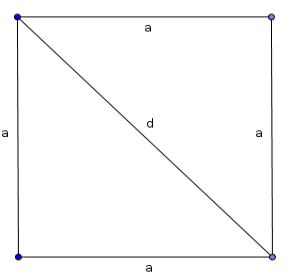
According to the Pythagorean theorem, the Pythagoreans knew that the diagonal could be calculated by1 \[d=\sqrt{2}\cdot a.\] They strongly believed that \(d\) would be commensurable with \(a\), i.e. a whole multiple \(a\) of \(\sqrt 2\) would produce another whole number \(d\), in other words \[a\cdot\sqrt 2=d\quad\text{or}\quad\sqrt 2=\frac da.\]
Some legends say that the Pythagorean Hippassus of Metapontum discovered the incommensurablility of the diagonal of a square. When the other Pythagoreans heard of his discovery, they decided to drown him at sea, because this discovery destroyed their belief in the commensurability of all geometric magnitudes.
The discovery of incommensurability of magnitudes is strongly linked to the discovery of irrational numbers, i.e. numbers that cannot be represented by a ratio of two whole numbers. This part of BookOfProofs is dedicated to irrational numbers and their properties.
The Pythagoreans neither knew the square root nor used the symbol \(\sqrt {}\) as we do today. However, they were able to construct the diagonal of the square and also knew the corresponding relationship according to the Pythagorean theorem, that given a square with a side \(a\), the sum of two such squares would equal the square of the diagonal \(d\): \[d^2=a^2+a^2.\] ↩