Proof: By Euclid
(related to Proposition: Prop. 10.094: Side of Area Contained by Rational Straight Line and Fourth Apotome)
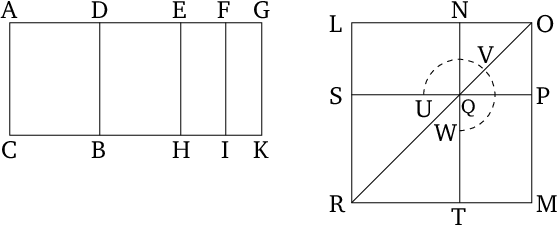
- For let $DG$ be an attachment to $AD$.
- Thus, $AG$ and $DG$ are rational (straight lines which are) commensurable in square only [Prop. 10.73], and $AG$ is commensurable in length with the (previously) laid down rational (straight line) $AC$, and the square on the whole, $AG$, is greater than (the square on) the attachment, $DG$, by the square on (some straight line) incommensurable in length with ($AG$) [Def. 10.14] .
- Therefore, since the square on $AG$ is greater than (the square on) $GD$ by the (square) on (some straight line) incommensurable in length with ($AG$), thus if (some area), equal to the fourth part of the (square) on $DG$, is applied to $AG$, falling short by a square figure, then it divides ($AG$) into (parts which are) incommensurable (in length) [Prop. 10.18].
- Therefore, let $DG$ have been cut in half at $E$, and let (some area), equal to the (square) on $EG$, have been applied to $AG$, falling short by a square figure, and let it be the (rectangle contained) by $AF$ and $FG$.
- Thus, $AF$ is incommensurable in length with $FG$.
- Therefore, let $EH$, $FI$, and $GK$ have been drawn through $E$, $F$, and $G$ (respectively), parallel to $AC$ and $BD$.
- Therefore, since $AG$ is rational, and commensurable in length with $AC$, the whole (area) $AK$ is thus rational [Prop. 10.19].
- Again, since $DG$ is incommensurable in length with $AC$, and both are rational (straight lines), $DK$ is thus a medial (area) [Prop. 10.21].
- Again, since $AF$ is incommensurable in length with $FG$, $AI$ (is) thus also incommensurable with $FK$ [Prop. 6.1], [Prop. 10.11].
- Therefore, let the square $LM$, equal to $AI$, have been constructed.
- And let $NO$, equal to $FK$, (and) about the same angle, $LPM$, have been subtracted (from $LM$).
- Thus, the squares $LM$ and $NO$ are about the same diagonal [Prop. 6.26].
- Let $PR$ be their (common) diagonal, and let the (rest of the) figure have been drawn.
- Therefore, since the (rectangle contained) by $AF$ and $FG$ is equal to the (square) on $EG$, thus, proportionally, as $AF$ is to $EG$, so $EG$ (is) to $FG$ [Prop. 6.17].
- But, as $AF$ (is) to $EG$, so $AI$ is to $EK$, and as $EG$ (is) to $FG$, so $EK$ is to $FK$ [Prop. 6.1].
- Thus, $EK$ is in mean proportion3 to $AI$ and $FK$ [Prop. 5.11].
- And $MN$ is also in mean proportion3 to the squares $LM$ and $NO$ [Prop. 10.13 lem.] , and $AI$ is equal to $LM$, and $FK$ to $NO$.
- $EK$ is thus also equal to $MN$.
- But, $DH$ is equal to $EK$, and $LO$ is equal to $MN$ [Prop. 1.43].
- Thus, the whole of $DK$ is equal to the gnomon $UVW$ and $NO$.
- Therefore, since the whole of $AK$ is equal to the (sum of the) squares $LM$ and $NO$, of which $DK$ is equal to the gnomon $UVW$ and the square $NO$, the remainder $AB$ is thus equal to $ST$ - that is to say, to the square on $LN$.
- Thus, $LN$ is the square root of area $AB$.
- I say that $LN$ is the irrational (straight line which is) called minor.
- For since $AK$ is rational, and is equal to the (sum of the) squares $LP$ and $PN$, the sum of the (squares) on $LP$ and $PN$ is thus rational.
- Again, since $DK$ is medial, and $DK$ is equal to twice the (rectangle contained) by $LP$ and $PN$, thus twice the (rectangle contained) by $LP$ and $PN$ is medial.
- And since $AI$ was shown (to be) incommensurable with $FK$, the square on $LP$ (is) thus also incommensurable with the square on $PN$.
- Thus, $LP$ and $PN$ are (straight lines which are) incommensurable in square, making the sum of the squares on them rational, and twice the (rectangle contained) by them medial.
- $LN$ is thus the irrational (straight line) called minor [Prop. 10.76].
- And it is the square root of area $AB$.
- Thus, the square root of area $AB$ is a minor (straight line).
- (Which is) the very thing it was required to show.
∎
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

- non-Github:
- @Fitzpatrick
References
Adapted from (subject to copyright, with kind permission)
- Fitzpatrick, Richard: Euclid's "Elements of Geometry"
