(related to Proposition: Cauchy Product of Absolutely Convergent Series)
We begin the proof with a number of definitions: We set
\[\begin{array}{c} A:=\sum_{n=0}^\infty a_n,\quad A_n:=\sum_{k=0}^n a_k\\ B:=\sum_{n=0}^\infty b_n,\quad B_n:=\sum_{k=0}^n b_k\\ c_n:=\sum_{k=0}^n a_{n-k}b_k,\quad C_n:=\sum_{k=0}^n c_k\\ D_n:=\left(\sum_{k=0}^n a_k\right)\left(\sum_{k=0}^n b_k\right)=A_n\cdot B_n\\ D_n^*:=\left(\sum_{k=0}^n |a_k|\right)\left(\sum_{k=0}^n |b_k|\right). \end{array}\]
The proof is in two steps:
By hypothesis, \(A\) and \(B\) are absolutely convergent series, which by definition means that \(\sum_{n=0}^\infty |a_n|\) and \(\sum_{n=0}^\infty |b_n|\) are convergent series. Due to the rule of the product of convergent sequences, it follows that the real sequences \((D_n^*)_{n\in\mathbb N}\) is a convergent sequence. This in turn means by definition that for a fixed \(\epsilon > 0\) there is an index \(m\in\mathbb N\) with \[|D_n^*- D_m^*| < \epsilon\]
for all $n\ge m$ and, in particular, for all $n > 2m.$ Note that if \( n > 2m \), then1 \[\begin{array}{rcl} D_n^* - D_m^*&=&\sum_{\substack{0\le i\le n \\ 0\le j\le n}} |a_i||b_j|-\sum_{\substack{0\le i\le m \\ 0\le j\le m}} |a_i||b_j|\\ &=&\sum_{i,j} |a_i||b_j|[0\le i\le n\wedge 0\le j\le n]-\sum_{i,j}|a_i||b_j|[0\le i\le m\wedge 0\le j\le m]\\ &=&\sum_{i,j} |a_i||b_j|[m < i \le n\wedge m < j\le n].\quad\quad ( * ) \end{array}\]
We will use this as an interim result.
Now, observe that first: \[D_n=\left(\sum_{k=0}^n a_k\right)\left(\sum_{k=0}^n b_k\right)=\sum_{\substack{0\le i\le n \\ 0\le j\le n}} a_ib_j=\sum_{i,j} a_ib_j[0\le i\le n\wedge 0\le j\le n]\] and that second \[C_n=\sum_{k=0}^n c_k=\sum_{k=0}^n \sum_{j=0}^k a_{k-j}b_j=\sum_{k=0}^n \sum_{i+j=k} a_ib_j=\sum_{i+j\le n} a_ib_j=\sum_{i,j} a_ib_j[i+j\le n]\] and that third, according to the triangle inequality and the properties of the absolute value. \[\begin{array}{rcl} |D_n - C_n|&=&\left|\sum_{i,j} a_ib_j[0\le i\le n\wedge 0\le j\le n] - \sum_{i,j} a_ib_j[i+j\le n]\right|\\ &=&\left|\sum_{i,j} a_ib_j[0\le i\le n\wedge 0\le j\le n\wedge i+j > n]\right|\\ &\le &\sum_{i,j} |a_i||b_j|[0\le i\le n\wedge 0\le j\le n\wedge i+j > n]\quad\quad ( * * ) \end{array}\] This is our second interim result.
Now, once again since \(A\) and \(B\) are absolutely convergent series, they are in particular convergent. Therefore, the real sequences of their partial sums \((A_n)_{n\in\mathbb N}\) and \((B_n)_{n\in\mathbb N}\) are convergent sequences with \(\lim A_n=A\) and \(\lim B_n=B\). Like in the reasoning above, due to the rule of the product of convergent sequences, we have \[\lim_{n\rightarrow\infty} D_n=\lim_{n\rightarrow\infty} (A_n \cdot B_n)=\lim_{n\rightarrow\infty} A_n \cdot \lim_{n\rightarrow\infty} B_n=A\cdot B.\] Thus, it suffices to demonstrate that \[\lim_{n\to\infty} (D_n - C_n)=0.\] But this will follow immediately, if we can show that for a given \(\epsilon > 0\) and all \(n > 2m\) the set of possible index pairs \(\{(i,j)\}\) in the sum \( ( * * ) \) is included in the set of index pairs \(\{(i,j)\}\), which are possible in the sum \( ( * ) \). If this is the case, the inequality \[|D_n - C_n| \le |D_n^*- D_m^*| < \epsilon\text{ for all }n\ge 2m\] will be true. But the set of possible index pairs \(\{(i,j)\}\) in the sum \( ( * * ) \) is indeed included in the set of index pairs \(\{(i,j)\}\), which are possible in the sum \( ( * ) \), like demonstrated in the following figure
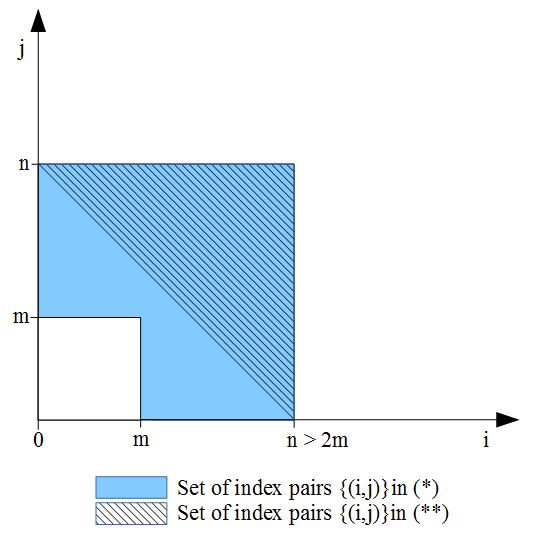
This is a pure geometric argument, since for \(n > 2m\) the hatched area is totally included in the blue area. Therefore, we have \(\lim_{n\to\infty} (D_n - C_n)=0,\) and \(\lim_{n\to\infty} C_n=A\cdot B\).
We have to show that \(\sum_{n\to\infty}|c_n|\) is convergent. It has already been shown that the real sequence \((D_n^*)_{n\in\mathbb N}\) is a convergent sequence. Moreover, we have in the Iverson notation
\[D_n^*=\sum_{i,j} |a_i||b_j|[0\le i\le n\wedge 0\le j\le n].\quad\quad ( \times )\]
On the other hand, it follows from the triangle inequality that \[\sum_{k=0}^n |c_k|=\sum_{k=0}^n \left|\sum_{j=0}^k a_{k-j}b_j\right|\le \sum_{k=0}^n \sum_{i+j=k} |a_i||b_j|=\sum_{i,j} |a_i||b_j|[i+j\le n]\quad\quad ( \times\times )\]
Following a similar geometric argument as above, the set of of possible index pairs \(\{(i,j)\}\) in the sum \( ( \times\times ) \) is included in the set of index pairs \(\{(i,j)\}\), which are possible in the sum \( ( \times ) \) - see following figure
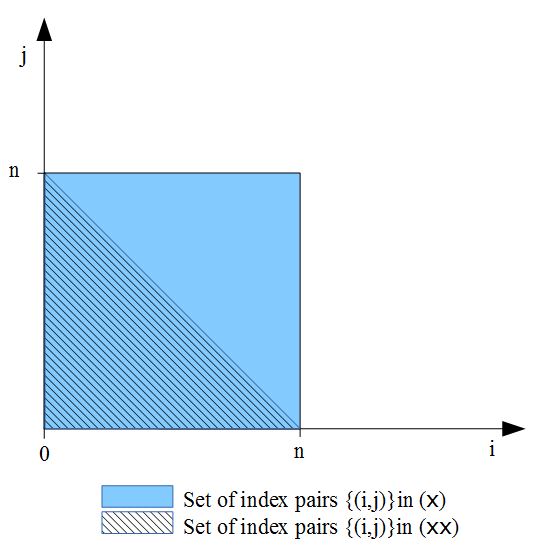
Therefore, we have
\[\sum_{k=0}^n |c_k|\le D_n^*\] and it follows from the majorant criterion that \(\sum_{n\to\infty}|c_n|\) is convergent.
In the following text, the Iverson notation for sum is used, which turns out to be very helpful in sum manipulation steps. ↩